原文始发于360漏洞研究院 戴建军:Math.abs JIT Optimization Bug in JSC
2021年天府杯我们成功完成iPhone 13 pro RCE的目标,这篇文章将会详细介绍其中使用到的Safari JavaScriptCore(JSC) 漏洞,漏洞编号为CVE-2021-30953。
ArithNegate
在JSC的JIT FTL优化过程中,对于 -n 的表达式会生成ArithNegate opcode,且ArithNegate会伴随相应的ArithMode,ArithMode有如下几种定义:
enum Mode {
NotSet, // Arithmetic mode is either not relevant because we're using doubles anyway or we are at a phase in compilation where we don't know what we're doing, yet. Should never see this after FixupPhase except for nodes that take doubles as inputs already.
Unchecked, // Don't check anything and just do the direct hardware operation.
CheckOverflow, // Check for overflow but don't bother with negative zero.
CheckOverflowAndNegativeZero, // Check for both overflow and negative zero.
DoOverflow // Up-convert to the smallest type that soundly represents all possible results after input type speculation.
};相信从注释中大家也能明白他们的含义,这里我们主要关注Unchecked和CheckOverflow,顾名思义Unchecked表示不需要对ArithNegate操作做任何检查,CheckOverflow则需要检查是否产生溢出。那么 -n 操作为什么需要检查溢出呢?什么数据能导致 -n 操作产生溢出呢?
我们都知道在INT32类型中,有一个INT_MIN,它的实际值是-2147483648,在JSC中,-(-2147483648)的结果会是什么呢?我们来看一个例子:
n = -2147483648 (INT_MIN)
let y = -n; // 2147483648 in 64bit value
let z = -n; // -2147483648 in 32 bit value, but overflow check normally在JSC中,所有Number类型均采用64位浮点数表达,但是如果在JIT过程中n的类型是32位,则编译器会认为ArithNegate操作产生的结果也是32位的,且会附加上CheckOverflow的检查,所以当n=-2147483648时,-n的结果也会是-2147483648,如果此时ArithMode为CheckOverflow,则会发生bailout,如若ArithMode为Unchecked,则不会bailout。
我们来看看ArithNegate的JIT编译函数:
void compileArithNegate()
{
switch (m_node->child1().useKind()) {
case Int32Use: {
LValue value = lowInt32(m_node->child1());
LValue result;
if (!shouldCheckOverflow(m_node->arithMode()))
result = m_out.neg(value);
else if (!shouldCheckNegativeZero(m_node->arithMode())) {
CheckValue* check = m_out.speculateSub(m_out.int32Zero, value);
blessSpeculation(check, Overflow, noValue(), nullptr, m_origin);
result = check;
} else {
speculate(Overflow, noValue(), nullptr, m_out.testIsZero32(value, m_out.constInt32(0x7fffffff)));
result = m_out.neg(value);
}
setInt32(result);
break;
}从代码中也能看出,CheckOverflow会产生溢出检查的汇编代码,Unchecked则直接产生 neg 汇编指令。
CheckInBounds
JSC中针对数组的访问,FTL SSALowering优化阶段会引入一个index范围检查的opcode: CheckInBounds,相应的代码如下:
case GetByVal: {
lowerBoundsCheck(m_graph.varArgChild(m_node, 0), m_graph.varArgChild(m_node, 1), m_graph.varArgChild(m_node, 2));
break;
}
case PutByVal:
case PutByValDirect: {
Edge base = m_graph.varArgChild(m_node, 0);
Edge index = m_graph.varArgChild(m_node, 1);
Edge storage = m_graph.varArgChild(m_node, 3);
if (lowerBoundsCheck(base, index, storage))
break;
...
Node* length = m_insertionSet.insertNode(
m_nodeIndex, SpecInt32Only, op, m_node->origin,
OpInfo(m_node->arrayMode().asWord()), Edge(base.node(), KnownCellUse), storage);
checkInBounds = m_insertionSet.insertNode(
m_nodeIndex, SpecInt32Only, CheckInBounds, m_node->origin,
index, Edge(length, KnownInt32Use)); 编译 CheckInBounds 的函数如下:
void compileCheckInBounds()
{
speculate(
OutOfBounds, noValue(), nullptr,
m_out.aboveOrEqual(lowInt32(m_node->child1()), lowInt32(m_node->child2())));从代码中也可以看出,CheckInBounds实际就是检查 index>= 0 && index < array.length。
DFGIntegerRangeOptimization
JSC FTL优化的 DFGIntegerRangeOptimization阶段,会删除一些它认为冗余的溢出和范围检查,例如下面的代码:
for (var i = 0; i < array.length; ++i) array[i];运行到该阶段之前,循环体内相应的主要opcode如下:
CheckInBounds
GetByVal很显然从JS代码中可以看出,i 的范围是[0, array.length),所以DFGIntegerRangeOptimization认为CheckInBounds是可以删除掉的,经该阶段优化之后,循环体内的opcode只剩GetByVal。
GetByValDFGIntegerRangeOptimization通过for (var i = 0; i < array.length; ++i)建立两个关系:Relationship(i >=0)和Relationship(i < array.length),而这两个关系刚好满足优化CheckInBounds的条件,相关代码如下:
case CheckInBounds: {
auto iter = m_relationships.find(node->child1().node());
if (iter == m_relationships.end())
break;
bool nonNegative = false;
bool lessThanLength = false;
for (Relationship relationship : iter->value) {
if (relationship.minValueOfLeft() >= 0)
nonNegative = true; // (1)
if (relationship.right() == node->child2().node()) {
if (relationship.kind() == Relationship::Equal
&& relationship.offset() < 0)
lessThanLength = true;
if (relationship.kind() == Relationship::LessThan
&& relationship.offset() <= 0)
lessThanLength = true; // (2)
}
}
if (DFGIntegerRangeOptimizationPhaseInternal::verbose)
dataLogLn("CheckInBounds ", node, " has: ", nonNegative, " ", lessThanLength);
if (nonNegative && lessThanLength) {
executeNode(block->at(nodeIndex));
if (UNLIKELY(Options::validateBoundsCheckElimination()) && node->op() == CheckInBounds)
m_insertionSet.insertNode(nodeIndex, SpecNone, AssertInBounds, node->origin, node->child1(), node->child2());
// We just need to make sure we are a value-producing node.
node->convertToIdentityOn(node->child1().node()); // (3)
changed = true;
}
break;
}根据 (1) && (2) 优化CheckInBounds(3)。从上述代码中可以总结出这样一个结论:要想优化CheckInBounds,必须建立两个Relationships:index >=0 和 index < array.length。
The Bug
DFGIntegerRangeOptimization会通过如下代码给 i = ArithAbs(n) 建立 i >= 0的关系:
case ArithAbs: {
if (node->child1().useKind() != Int32Use)
break;
setRelationship(Relationship(node, m_zero, Relationship::GreaterThan, -1));
break;当 n < 0 且 Math.abs(n) 不会产生溢出的时候,DFGIntegerRangeOptimization会将 Math.abs(n)转化成 ArithNegate(n),且 ArithMode 为 Unchecked,相关代码如下:
case ArithAbs: {
if (node->child1().useKind() != Int32Use)
break;
...
executeNode(block->at(nodeIndex));
if (minValue >= 0) {
node->convertToIdentityOn(node->child1().node());
changed = true;
break;
}
bool absIsUnchecked = !shouldCheckOverflow(node->arithMode()); // (1)
if (maxValue < 0 || (absIsUnchecked && maxValue <= 0)) {
node->convertToArithNegate(); // (2)
if (absIsUnchecked || minValue > std::numeric_limits<int>::min())
node->setArithMode(Arith::Unchecked); // (3)
changed = true;
break;
}结合上述两段代码,如下实例代码会产生关系 i >= 0,且 Math.abs(n) 转换成 -n,但此时 ArithMode 为 CheckOverflow。
if(n < -1){
let i = Math.abs(n); // => (-n), CheckOverflow, i>=0;
}那么关键问题就在于:要想 -int_min 操作不会被检查CheckOverflow,即 ArithNegate 的 ArithMode被设置成Arith::Unchecked(3),则 ArithAbs 的 ArithMode也必须为 Arith::Unchecked。
此时问题转化成如何将 ArithAbs 的 ArithMode 设置成 Arith::Unchecked。
在Fixup阶段会设置 ArithAbs 的 ArithMode:
case ArithAbs: {
if (node->child1()->shouldSpeculateInt32OrBoolean()
&& node->canSpeculateInt32(FixupPass)) {
fixIntOrBooleanEdge(node->child1());
if (bytecodeCanTruncateInteger(node->arithNodeFlags())) // (1)
node->setArithMode(Arith::Unchecked);
else
node->setArithMode(Arith::CheckOverflow);
node->clearFlags(NodeMustGenerate);
node->setResult(NodeResultInt32);
break;
}如果满足条件(1),则会将 ArithMode 设置成 Unchecked。bytecodeCanTruncateInteger函数代码如下:
static inline bool bytecodeUsesAsNumber(NodeFlags flags)
{
return !!(flags & NodeBytecodeUsesAsNumber);
}
static inline bool bytecodeCanTruncateInteger(NodeFlags flags)
{
return !bytecodeUsesAsNumber(flags);
}此时问题转化成如何将 ArithAbs 的 NodeFlags设置成 ~NodeBytecodeUsesAsNumber。
而 NodeFlags 的设置操作发生在 BackwardsPropagation阶段:
case ArithBitOr: //(1)
case ArithBitXor:
case ValueBitAnd:
case ValueBitOr:
case ValueBitXor:
case ValueBitLShift:
case ArithBitLShift:
case ArithBitRShift:
case ValueBitRShift:
case BitURShift:
case ArithIMul: {
flags |= NodeBytecodeUsesAsInt;
flags &= ~(NodeBytecodeUsesAsNumber | NodeBytecodeNeedsNegZero | NodeBytecodeUsesAsOther);
flags &= ~NodeBytecodeUsesAsArrayIndex;
node->child1()->mergeFlags(flags); // (2)
node->child2()->mergeFlags(flags);
break;
}ArithBitOr 的操作会将 ArithBitOr->child1->flags 设置成 ~NodeBytecodeUsesAsNumber。
结合BackwardsPropagation阶段的代码来看看如下实例:
if(n < -1){
let i = Math.abs(n) | 0;
}此时 ArithBitOr->child1() 即是 ArithAbs(n),那么ArithAbs(n)->flags 会 merge( ~NodeBytecodeUsesAsNumber),将 ArithAbs 的 NodeFlags设置成 ~NodeBytecodeUsesAsNumber。然而 DFGIntegerRangeOptimization 阶段并没有 ArithBitOr 的优化处理,则 Math.abs(n)>= 0 的关系并不会传递到 i 。
此时问题转化成如何将 Math.abs(n) | 0 转换成 Math.abs(n)。
StrengthReduction 阶段解决了该问题:
case ArithBitOr:
handleCommutativity();
if (m_node->child1().useKind() != UntypedUse && m_node->child2()->isInt32Constant() && !m_node->child2()->asInt32()) {
convertToIdentityOverChild1(); // (1)
break;
}
break;当 ArithBitOr->child2() 等于0时,ArithBitOr 被转换成 child1(),从而 Math.abs(n) | 0 转换成 Math.abs(n)。
把上述涉及到的几个优化阶段串联起来:

结合上述的优化流程,如下实例代码则成功优化 CheckInBounds:
function jit(arr, n) {
// Force n to be a 32bit integer
n |= 0;
if (n < -1) {
let i = Math.abs(n)|0; // (1) i >= 0, Unchecked
if (i < arr.length) { // (2) i < array.length
arr[i] = 1.04380972981885e-310; // (3) remove CheckInBounds
}
}
}代码(1)建立关系 i >= 0;代码(2)建立关系 i < arr.length,则代码(3)处的 CheckInBounds会被优化。
再结合文章开始分析的,当 n = -2147483648 时,i = -n = -2147483648,整数溢出不会被检查,而此时 arr[i] 也没有CheckInBounds检查,则发生越界写。
Exploit
漏洞利用采用比较常规的方法,通过越界写完成addrOf 和 fakeObj 两个原语,再结合 Samuel Groß介绍的方法完成任意地址读写。JSC公开的利用方法有很多,在这里就不详细介绍了。
Patch
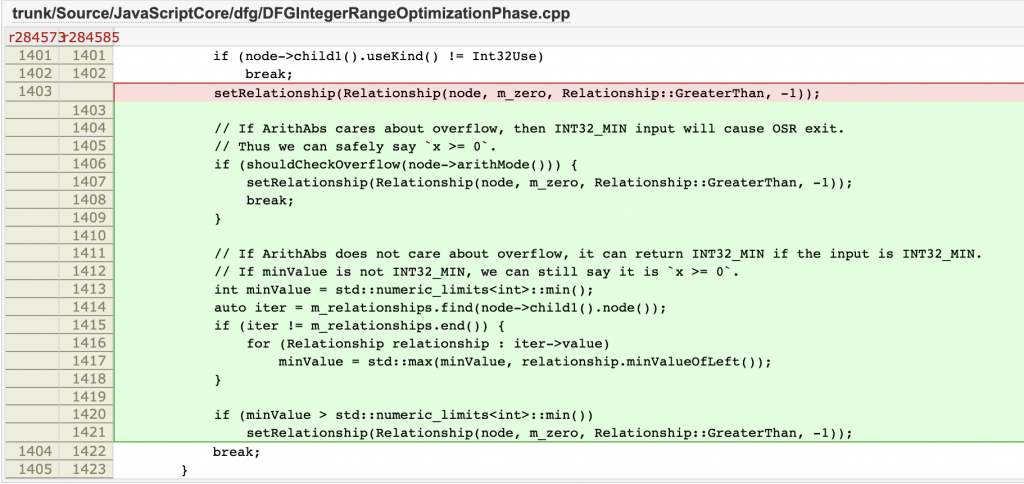
DFGIntegerRangeOptimization 在创建 ArithAbs >= 0关系时,增加了对 ArithMode 和最小值的检查。
Conclusion
本文对CVE-2021-30953的成因进行了分析,详细介绍了漏洞涉及到的全部优化过程,文章最后简单介绍了漏洞利用方法和漏洞修复方法。