CTF导航 CTF导航

信息安全算法基础

区块链安全 2年前 (2022) admin
416 0 0

信息安全算法基础

前言

这篇文章是电子科技大学，计算机科学与工程学院，网络空间安全专业的《信息安全基础综合设计实验》的总结。本人将它视为复习总结，读者可以当作学习使用 C++ 编写密码学函数和使用密码学库的入门资料。由于包含了课程作业答案，所以明年的这个时候应该会隐藏文章。

数论基础

模指数运算

主要就是分治算法，避免计算过程中溢出。递归的写法要注意堆栈溢出，因为当 e 不等于 0 的时候，每一层递归都会有两个分叉，也就是 2^32 次方的话，就会有 2^32 次方分叉，程序非常慢。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
 
unsigned int mod_exp(unsigned int a,unsigned int e, unsigned int n) {

	if(e==0) {
		return 1;
	}

	if(e%2 == 0) {
		return mod_exp(a,e/2,n)%n*(mod_exp(a,e/2,n)%n)%n;
	} else {
		return mod_exp(a,e/2,n)%n *(mod_exp(a,e/2,n)%n)%n*(a%n)%n;
	}
}

那么还是采用 power 函数，那么就只有线性复杂度了。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
 
unsigned int mod_exp(unsigned int a,unsigned int e, unsigned int n) {

	if(e==0) {
		return 1;
	}

	if(e%2 == 0) {
		return (unsigned int)pow(double(mod_exp(a,e/2,n)%n),2)%n;
	} else {
		return (unsigned int)pow(double(mod_exp(a,e/2,n)%n),2)%n*(a%n)%n;
	}

}

另外，用循环编写也是可以的，只需要把指数当作二进制，从低位开始扫描，遇到 0 就不处理，遇到 1 就翻倍，然后每次扫描都通过之前的 n 次方的值，计算 2n 次方的值。二进制数的话，就通过 mod 2 和 /2 去实现。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
unsigned int mod_exp(unsigned int a,unsigned int e, unsigned int n) {
	unsigned int val= a%n;
	unsigned int res =1;
	while(e!=0){
		if(e%2==1){
			res = res*val%n;
		}
		val = (val%n)*(val%n)%n;
		e/=2;
	}

	return res;

}

Eratosthenes 素性检测

通过 Eratosthenes 找出 {2,3,⋯,n1/2} 中的素数，判断 n 是否含有这些素因子。Eratosthenes 筛选法主要是确定 1 和 2 是素数，然后去除 2 的倍数。接着找到下一个数，继续去除这个数的倍数。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
 
bool is_prime[100000];
bool Eratosthenes(unsigned int a) {
	memset(is_prime, 1, 100000*sizeof(bool));//初始都没有被筛除
	if(a==1 || a==0) return false;

	unsigned int sqr = (unsigned int)sqrt(double(a));
	int i;
    for(i = 2;i <= sqr;i++){
        if(!is_prime[i]) continue; // 如果这个数已经被去除了，就不会用到它
        for(int j = 2; i*j<=sqr;j++){ //筛选倍数
            if(is_prime[i*j]) is_prime[i*j] = false;
        }
        //如果是素数，那么计算整除
        if(a%i==0){
            return false;
        }
    }
    return true;
}

Miller-Rabin 素性检测

任意的素数都可以表示成 为奇数2kq+1,k⩾0,q为奇数 的形式，又素数 n 满足费马小定理定理

 

an−1modn=a2kqmodn=1,1<a<n−1

 

然后由因式分解。

 

0=a2kq−1=(a2k−1q−1)(a2k−1q+1)=(aq−1)∏j=1k(a2j−1q+1)modn

 

所以对于给定的 a，如果 n 是素数，那么一定满足一下条件之一：

  • aqmodn=1
  • ∃j,1⩽j⩽k,a2j−1q=n−1modn

所以，如果都不满足这两个条件，那么 n 必然不是素数。但是如果满足也不一定是素数。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
 
bool Miller_Rabin(unsigned int n,unsigned a) {
    unsigned int tmp = n-1;
    unsigned int k,q;
    k=0;
    while(tmp%2!=0){
        k++;
        tmp/=2;
    }
    q=tmp;
    if(mod_exp(a,q,n) == 1) {
        return true;
    }
    for(int j=1;j<=k;j++){
        if(mod_exp(a,mod_exp(2,j-1,1)*q,n)==n-1){
            return true;
        }
    }

    return false;
}

乘法逆元

详细过程参考笔记，实际考试的时候大概率记住最好。这也是没办法的事情，考试主要是记忆已有的东西。记住基本递归形式，记住每次回溯的方式。特别注意溢出的问题，特别是采用 unsigned int 时做减法

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
 
void extgcd(unsigned int a, unsigned int b, int &x, int &y){
    if(a==0){
        x = 0;
        y = 1;
        return;
    }
    extgcd(b%a,a,x,y);
    int t = x;
    x = y - b/a*x;
    y = t;
}

unsigned int gcd(unsigned int a, unsigned int b){
	if(a%b == 0){
		return b;
	}
	return gcd(b,a%b);
}

int reverse(unsigned int a, unsigned int n){
	if(!a||!n||gcd(a,n)!=1){
		return 0;
	}

	int x,y;
	extgcd(a,n,x,y);
	return x%n;
}

考试之前记得记一记。

伪随机数生成器

随机数具有随机性：均匀分布、难以重现，机器生成的一般时伪随机数。伪随机数生成器通过种子和确定性算法，生成不断迭代的伪随机序列，具有伪随机性、可重现

信息安全算法基础一般 C 语言生成随机数都是先 srand(seed) 设置种子，最常见的是 srand(time(NULL))

LCG

线性同余伪随机数生成器的基本结构是

 

xi+1=axi+cmodm

 

  • a 叫做乘数
  • c 叫做增量。
  • m 叫做模数。
  • x0 初始值叫做种子。

它生成的伪随机数具备以下性质：

  1. 不具备全周期性质。循环的长度不一定为 m-1，可能生成的随机数只有少数几个。
  2. 容易根据之前的随机数 x0,x1,⋯,xi−1 推断出 xi

所以线性同余位随机数生成器不具备可证明的安全性，可证明安全性指的是 可以将区分伪随机数和随机数规约为解决数学难题

BBS

BBS (Blum Blum Shub) 伪随机数生成器具备可证明安全性，基于大数难分解困难问题（给定 n，无法确定 n 的因子），结构如下：

 

xi=xi−12modn{n=pq,p≡q≡3mod4x0=s,gcd(s,n)=1

 

然后从 x0,x1,⋯,xi 中每个数选择重要的比特位（比如最低位、奇校验位、偶校验位），然后组成了一个 i+1 位的二进制序列。注意 x0 是最高位。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
 
unsigned int least_bit(unsigned int n){
	return n&0x0001;
}

unsigned int even_check_bit(unsigned int n){
	unsigned int cnt = 0;
	while(n!=0){
		cnt+=n%2;
		n /=2;
	}
	if(cnt%2==0){
		return 0;
	}
	return 1;
}

unsigned int odd_check_bit(unsigned int n){
	return 1 - even_check_bit(n);
}

unsigned int bbs(int flag){
	unsigned p,q,n,s,res;
	p=11,q=19,s=3,n=p*q;
	res = 0;
	unsigned int i;

	for(i=0;i<32;i++){
		s = (s%n)*(s%n)%n;
		unsigned int b;
		switch(flag){
			case 0:
				b = least_bit(s);
				break;
			case 1:
				b = odd_check_bit(s) ;
				break;
			case 2:
				b = even_check_bit(s);
				break;
		}
		res=res*2;
		res+= b;
	}
	return res;
}

另外，这里老师还介绍了微秒级别的获取时间的函数 gettimeofday，主要记得它的参数类型是 struct timeval：

 

 

1
2
3
4
5
6
7
8
9
10
11
 
int main() {
	struct timeval start,end;
	gettimeofday(&start,NULL);
	unsigned int a = (unsigned int)-1;
	cout<<bbs(0)<<endl;
	cout<<bbs(1)<<endl;
	cout<<bbs(2)<<endl;
	gettimeofday(&end,NULL);
	float time_use = (end.tv_sec - start.tv_sec) * 1000000 + (end.tv_usec - start.tv_usec);
	cout<< time_use<<endl;
}

不过，读者可以在 Linux 系统下用 man 命令获取相关信息。

非对称密码

从这一节开始，我们不再自己写算法，而是学会使用 openssl 库来实现密码学函数。

大数运算

大数运算时最基础的 openssl 内容，用于处理任意大的整数。在此之前，请检查是否按照密码学库，运行 sudo apt-get install libssl-dev。编译时需要引入库：gcc/g++ <源文件> -o <可执行文件> -lcrypto。这里主要使用<openssl/bn.h>。

创建和释放

 

 

1
2
3
4
5
6
7
8
9
10
11
 
 #include <openssl/bn.h>
//返回一个初始化了的 BIGNUM 类型的对象的指针，失败返回 NULL
 BIGNUM *BN_new(void);
//初始化已经分配了内存的 BIGNUM
 void BN_init(BIGNUM *);
//不释放内存，但是将变量赋值0
 void BN_clear(BIGNUM *a);
//释放内存
 void BN_free(BIGNUM *a);

 void BN_clear_free(BIGNUM *a);

下面是 CTX 也就是 context 类型，用于计算时暂存上下文，下面时创建和释放的方法。

 

 

1
2
3
 
#include <openssl/bn.h>
BN_CTX *BN_CTX_new(void);
void BN_CTX_free(BN_CTX *c);

基本赋值

 

 

1
2
3
4
5
6
7
8
9
 
int BN_zero(BIGNUM *a);
int BN_one(BIGNUM *a);

int BN_bn2bin(const BIGNUM *a, unsigned char *to);
BIGNUM *BN_bin2bn(const unsigned char *s, int len, BIGNUM *ret);
char *BN_bn2hex(const BIGNUM *a);
char *BN_bn2dec(const BIGNUM *a);
int BN_hex2bn(BIGNUM **a, const char *str);
int BN_dec2bn(BIGNUM **a, const char *str);
  • int 返回值 1 表示成功。转二进制或者十六进制的返回字符指针。
  • BN_bn2bin 中 to 字符串的长度必须是 BN_num_bytes(a)，而且是二进制输入。
  • 如果 *a 是 NULL，就会函数分配内存。
  • 转字符串的函数会返回 NULL 结尾的字符串。
  • 注意十六进制转 BIGNUM 是不带前缀 0x 的。

基本运算

r 表示结果，部分函数需要 ctx。BN_div 中 dv=a/d,rem=a%d，除了最简单的加减，最后一个参数都是 ctx。

 

 

1
2
3
4
5
6
7
8
9
10
11
 
int BN_add(BIGNUM *r, const BIGNUM *a, const BIGNUM *b);
int BN_sub(BIGNUM *r, const BIGNUM *a, const BIGNUM *b);
int BN_mul(BIGNUM *r, BIGNUM *a, BIGNUM *b, BN_CTX *ctx);
int BN_sqr(BIGNUM *r, BIGNUM *a, BN_CTX *ctx);
int BN_div(BIGNUM *dv, BIGNUM *rem, const BIGNUM *a, const BIGNUM *d,
           BN_CTX *ctx);
int BN_mod(BIGNUM *rem, const BIGNUM *a, const BIGNUM *m, BN_CTX *ctx);
int BN_exp(BIGNUM *r, BIGNUM *a, BIGNUM *p, BN_CTX *ctx);
int BN_gcd(BIGNUM *r, BIGNUM *a, BIGNUM *b, BN_CTX *ctx);

 BIGNUM *BN_mod_inverse(BIGNUM *r, BIGNUM *a, const BIGNUM *n, BN_CTX *ctx);

上面的许多运算都可以加入模运算，倒数第二个参数是模。

 

 

1
 
int BN_mod_add(BIGNUM *ret, BIGNUM *a, BIGNUM *b, const BIGNUM *m, BN_CTX *ctx);

比较函数

 

 

1
2
3
4
5
6
 
int BN_cmp(BIGNUM *a, BIGNUM *b); // -1 if a < b, 0 if a == b and 1 if a > b
int BN_ucmp(BIGNUM *a, BIGNUM *b); //比较绝对值
int BN_is_zero(BIGNUM *a);
int BN_is_one(BIGNUM *a);
int BN_is_word(BIGNUM *a, BN_ULONG w);
int BN_is_odd(BIGNUM *a);

综合运用

虽然 BIGNUM 内置了乘法逆元、模指数运算等函数，但是我们仍然可以自己实现一个自己的乘法逆元：

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
 
string big_mod_exp2(string a, string e, string m)
{
    BIGNUM *a1, *e1, *m1;
    BN_CTX *ctx = BN_CTX_new();
    a1 = e1 = m1 = NULL;
    BN_dec2bn(&a1, a.c_str());
    BN_dec2bn(&e1, e.c_str());
    BN_dec2bn(&m1, m.c_str());

    BIGNUM *t = BN_new();
    BIGNUM *res = BN_new();
    BN_one(res);
    BN_mod(t, a1, m1, ctx);
    while (!BN_is_zero(e1))
    {
        if (BN_is_bit_set(e1, 0))
        {

            BN_mod_mul(res, res, t, m1, ctx);
        }
        BN_rshift1(e1, e1);
        BN_mod_mul(t, t, t, m1, ctx);
    }
    return string(BN_bn2dec(res));
}

比较意外的是，自己实现的似乎比内置的更加高效，可能是占用内存更多一些，内置的占用内存更少一些。

RSA 加密

算法原理很简单，不赘述。

信息安全算法基础

直接使用

首先看生成密钥的方式，RSA_new 并不会生成一个直接可以用的密钥，还需要赋值。赋值的方式一种是分别对参数赋值，类似于 key->n = BN_bin2bn(rsaN, n_len, NULL); key->d = BN_bin2bn(rsaD, d_len, NULL); key->e = BN_bin2bn(rsaE, e_len, NULL);。另外一种就是下面的函数。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
 
#include <string.h>
#include <openssl/bn.h>
#include <openssl/rsa.h>
#include "iostream"
using namespace std;
int main()
{
    unsigned char a[]="asdfg123sda/.,";
    RSA *key = RSA_new();
    key = RSA_generate_key(1024,0x100001,NULL,NULL);

    unsigned char * cipher = (unsigned char *)malloc(RSA_size(key));
    unsigned char * res = (unsigned char *)malloc(RSA_size(key));

    int cipher_len = RSA_public_encrypt(strlen((char*)a),a,cipher,key,RSA_PKCS1_PADDING);
    int plain_len =RSA_private_decrypt(cipher_len,cipher,res,key,RSA_PKCS1_PADDING);
    cout<<string((char*)res,plain_len)<<endl;

    return 0;
}

注意字符串的长度，因为加密和解密函数的字符串是没有 NULL 结尾的，创建 string 需要指定长度。

接着最常用的函数如下，具体的参数要求可以查看文档。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 
#include <openssl/rsa.h>
#include <openssl/engine.h>

RSA * RSA_new(void);
void RSA_free(RSA *rsa);

int RSA_public_encrypt(int flen, unsigned char *from, unsigned char *to, RSA *rsa, int padding);
int RSA_private_decrypt(int flen, unsigned char *from, unsigned char *to, RSA *rsa, int padding);
int RSA_private_encrypt(int flen, unsigned char *from, unsigned char *to, RSA *rsa,int padding);
int RSA_public_decrypt(int flen, unsigned char *from, unsigned char *to, RSA *rsa,int padding);

int RSA_sign(int type, unsigned char *m, unsigned int m_len, unsigned char *sigret, unsigned int *siglen, RSA *rsa);
int RSA_verify(int type, unsigned char *m, unsigned int m_len, unsigned char *sigbuf, unsigned int siglen, RSA *rsa);

int RSA_size(const RSA *rsa);

RSA *RSA_generate_key(int num, unsigned long e, void (*callback)(int,int,void *), void *cb_arg);
int RSA_print_fp(FILE *fp, RSA *x, int offset);

值得一提的是 RSA_print_fp 标准输出的东西，模数，公开的 e，私密的 d，两个大素数。后面的参数估计是为了简化运算，提前算出来的值。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
 
RSA Private-Key: (1024 bit, 2 primes)
modulus:
    00:c6:42:9c:69:e2:ef:6d:ed:9e:c6:2d:4b:ea:43:
    35:d9:94:14:e2:b0:e9:4e:66:24:c4:5b:df:96:23:
    ef:5d:67:46:7c:7e:ab:ff:05:5d:17:de:3f:00:d1:
    67:f3:6a:b0:0c:89:f2:40:b9:11:0a:7d:c6:3a:23:
    91:82:f8:c7:75:ce:3c:8c:19:f0:3e:7e:a9:fa:07:
    a5:87:05:81:3e:51:cc:88:9e:0a:e1:34:50:77:34:
    bb:c1:9c:bf:75:d8:54:18:fa:db:c6:74:fc:a3:60:
    cc:44:fb:60:ea:b9:f4:68:f5:d9:11:8a:82:f8:a4:
    c6:59:9b:82:28:2c:7c:72:1b
publicExponent: 1048577 (0x100001)
privateExponent:
    00:bd:2e:ab:b0:33:d0:38:db:c7:08:71:50:52:68:
    bc:05:c5:8f:9b:c9:0a:8a:26:59:3c:df:f0:24:d3:
    c0:ba:68:18:5c:f9:c4:28:be:54:5d:59:44:50:20:
    3c:67:42:e7:ff:ef:79:14:04:7a:8b:47:74:64:3a:
    b2:75:a2:c2:ad:7c:11:4c:a5:48:89:2b:86:fa:e5:
    6e:bd:2e:04:d6:e9:34:70:ef:d2:57:f8:cf:5d:93:
    57:ba:b2:2a:3d:fd:3a:f0:88:27:4c:e5:5b:77:b9:
    cc:b1:a0:4e:8a:fa:f4:51:38:49:e8:24:c7:2e:a2:
    1d:9d:08:4f:22:54:ed:ab:79
prime1:
    00:fa:58:0e:cc:a1:cc:bc:38:d5:99:02:7e:2e:6a:
    d0:3a:fe:40:bd:13:ea:5e:27:7d:8b:1a:77:d5:c3:
    e8:13:09:f9:fc:9c:b8:db:15:e8:8b:39:03:74:66:
    ef:9a:03:e5:a5:38:af:51:b0:2d:e0:fb:90:f1:b9:
    45:00:f5:da:6f
prime2:
    00:ca:bd:4f:7b:09:86:08:95:81:28:65:38:a7:fe:
    c6:bb:d7:5c:3a:95:ca:c0:cb:6d:97:8f:aa:f6:18:
    91:07:8e:18:c8:5d:02:30:f8:fa:7c:87:53:41:6d:
    80:0d:3b:ae:6d:ff:3a:33:a4:e4:61:e0:6b:bd:8f:
    d1:1e:e6:69:15
exponent1:
    00:d7:1b:cc:85:a7:de:88:dd:0d:3b:00:88:ab:e9:
    cc:dd:93:d9:d7:39:97:55:fd:89:47:c5:d1:ab:98:
    92:97:92:d1:0c:19:b9:34:e4:67:da:1a:27:8e:4a:
    59:cc:38:ec:77:40:c5:70:ac:82:e1:20:fa:a1:23:
    ff:70:6b:49:01
exponent2:
    59:50:33:aa:45:b5:a4:35:38:50:5e:e0:59:4d:de:
    6a:1a:a7:2a:d1:91:d2:69:10:bb:13:39:e4:71:b0:
    be:cb:bc:7c:aa:77:60:38:fc:df:63:94:86:49:ab:
    64:59:ac:20:30:cd:59:fa:e6:8f:72:c3:27:68:24:
    6e:9d:44:71
coefficient:
    00:e0:01:b8:44:3e:26:66:05:dc:ab:6d:07:cf:63:
    0b:72:25:ce:3e:8f:d6:61:be:f4:c9:57:b1:a3:b4:
    7d:e4:7f:20:7d:5b:25:27:aa:d6:07:8f:0e:46:3e:
    76:ba:15:e1:67:25:1b:10:3e:7b:87:1d:28:e1:79:
    03:de:cc:96:ab

从文件读取

从文件读取然后创建密钥，特别是区分公钥和私钥。我们只学了两个函数，分别用于读取公钥和私钥PEM_read_RSA_PUBKEY、PEM_read_RSAPrivateKey。这两个函数的大小写怪怪的，考试前要记一下，因为不同格式的 PEM 文件要用不同的函数读取。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 
RSA *createRSAWithFilename(char *filename, int is_pub) {
    FILE *fp = fopen(filename, "rb");
    if (fp == NULL) {
        printf("Unable to open file %s \n", filename);
        return NULL;
    }
    RSA *rsa = RSA_new();
    if (is_pub) {
        rsa = PEM_read_RSA_PUBKEY(fp, &rsa, NULL, NULL);
//        rsa = PEM_read_RSAPublicKey(fp, &rsa, NULL, NULL); //这是另外一种格式的 PEM 读取方式。
    } else {
        rsa = PEM_read_RSAPrivateKey(fp, &rsa, NULL, NULL);
    }
    fclose(fp);
    return rsa;
}

给出完整的加解密代码：

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
 
string RSA_Encrypt(string plaintext, string pub_key_file) {
    FILE *f = fopen(pub_key_file.c_str(), "rb");
    if (f == NULL) {
        printf("load public key failed!");
    }
    RSA *key = RSA_new();
    key = PEM_read_RSA_PUBKEY(f, NULL, NULL, NULL);
    if (key == NULL) {
        printf("generate public key failed!");
    }
    unsigned char *cipher = (unsigned char *) malloc(RSA_size(key));
    int cipher_len = RSA_public_encrypt(plaintext.length(), (const unsigned char *) plaintext.c_str(), cipher, key, RSA_PKCS1_PADDING);
    return string((char *) cipher, cipher_len);
}

string RSA_Decrypt(string ciphertext, string pub_key_file) {
    FILE *f = fopen(pub_key_file.c_str(), "rb");
    if (f == NULL) {
        printf("load private key failed!");
    }
    RSA *key = RSA_new();
    key = PEM_read_RSAPrivateKey(f, NULL, NULL, NULL);
    if (key == NULL) {
        printf("generate private key failed!");
    }
    unsigned char *plain = (unsigned char *) malloc(RSA_size(key));
    int plain_len = RSA_private_decrypt(ciphertext.length(), (const unsigned char *) ciphertext.c_str(), plain, key, RSA_PKCS1_PADDING);
    return string((char *) plain, plain_len);
}

RSA 签名

我们知道私钥用于签名，公钥用于验证。我们可以使用内置的函数，更加方便，也更加实用。

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
 
string sign(string data, string private_key_file) {
    FILE *f = fopen(private_key_file.c_str(), "rb");
    if (f == NULL) {
        printf("load private key failed!");
    }
    RSA *key = RSA_new();
    key = PEM_read_RSAPrivateKey(f, NULL, NULL, NULL);
    fclose(f);
    if (key == NULL) {
        printf("generate private key failed!");
    }
    unsigned char *sig = (unsigned char *) malloc(RSA_size(key));
    unsigned int sig_len;
    if (!RSA_sign(NID_sha1, (const unsigned char *) data.c_str(), data.length(), sig, &sig_len, key)) {
        printf("sign failed!");
    }
    return string((char *) sig, sig_len);
}

string verify(string data, string signature, string pub_key_file) {
    FILE *f = fopen(pub_key_file.c_str(), "rb");
    if (f == NULL) {
        printf("load public key failed!");
    }
    RSA *key = RSA_new();
    key = PEM_read_RSA_PUBKEY(f, NULL, NULL, NULL);
    fclose(f);
    if (key == NULL) {
        printf("generate public key failed!");
    }

    if (!RSA_verify(NID_sha1, (const unsigned char *) data.c_str(), data.length(),
                    (unsigned char *) signature.c_str(), signature.length(), key)) {
        return "verify failed!";
    }
    return "verify success!";
}

对称密码

因为课堂教学顺序是这样，所以我也放在最后了。

RC4

流密码是对称加密算法，加解密双方（基于密钥）产生相同伪随机流， 明文与伪随机流按位异或加密。一种具有可变密钥长度（1~255 字节）的流密码。它依赖初始的 256 字节状态数组（初始化为单位数组）开始迭代

  • KSA 算法：基于 K 置换状态数组
  • PRNG 算法：扩充状态数组，加密明文数据

 

 

1
2
3
4
5
6
7
 
string rc4_encrypt(string data,string init_key){
    RC4_KEY key;
    RC4_set_key(&key,init_key.length(),(const unsigned char*)init_key.c_str());
    unsigned char* cipher = (unsigned char *) malloc(sizeof(unsigned char) * (data.length()));;
    RC4(&key,data.length(),(const unsigned char*)data.c_str(),cipher);
    return string((char*)cipher,data.length());
}

需要注意两个地方，RC4_KEY 不能是指针，必须声明式结构体。接收密文的 buffer 必须提前分配和明文一样大的内存。

DES

DES 是分组密码，将明文进行分组，将每个明文分组作为整体进行加解密。分组长度 64 位；有效密钥长度 56 位。DES 基于 Feistel 密码结构，也就是

  • 扩散：明文每一位影响密文许多位
  • 混淆：隐藏密文与密钥统计关系

分组密码应用模式

  • ECB(Electronic codebook)，每个分组都是各自独立加密的，不好隐藏数据的模式和统计特征。
  • CBC(Cipher-block chaining)，第一个块需要使用初始化向量，然后每个密文块依赖上一个密文块。串行加密，并行解密。信息安全算法基础信息安全算法基础
  • CTR(Counter mode)，数器可以是任意保证长时间不产生重复输出的函数，但使用一个普通的计数器是最简单和最常见的做法。并行加密，并行解密。信息安全算法基础信息安全算法基础

代码

核心就是记得 DES_string_to_key 之后再 DES_set_key_checked 生成另外一个密钥，加密函数的最后一个参数要写 DES_ENCRYPT 或者 DES_DECRYPT

 

 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
 
void convert_string_to_des_block(string str, DES_cblock &output) {
    for (int i = 0; i < 8; ++i) output[i] = str[i];
}

//只能处理一个8字节的块，需要加密任意数据的话，还需要封装一层
string des_encrypt(string plain, string secret_key) {
    DES_cblock in_data, out_data, key;
    convert_string_to_des_block(plain, in_data);
    DES_string_to_key(secret_key.c_str(), &key);
    DES_key_schedule keys;
    DES_set_key_checked(&key, &keys);

    DES_ecb_encrypt(&in_data, &out_data, &keys, DES_ENCRYPT);
    return string((char *) out_data, plain.length());
}

SHA-1

哈希函数单向、抗碰撞，用于检测数据完整性。考前要记住 SHA1，摘要 160 bit，分组 521 bit，80 次迭代。

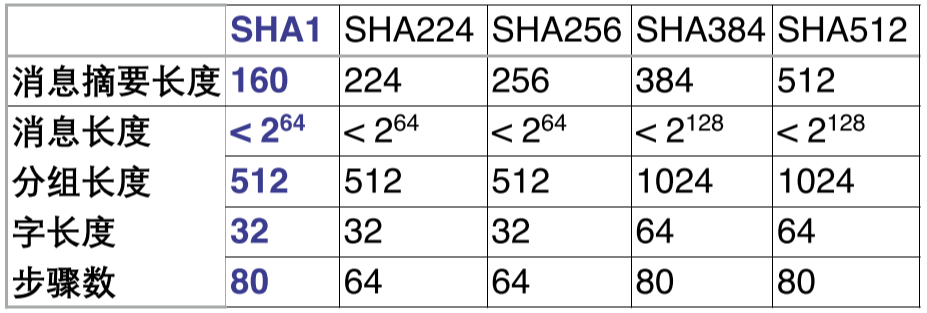
信息安全算法基础

代码挺简单的，注意缓冲区 20 字节就可以了。

 

 

1
2
3
4
5
 
string sha1_digest(string msg) {
    unsigned char obuf[20];
    SHA1((unsigned char *) msg.c_str(), msg.length(), obuf);
    return string((char *) obuf, 20);
}

 

原文始发于learner L：信息安全算法基础

版权声明：admin 发表于 2022年12月6日 上午10:00。
转载请注明：信息安全算法基础 | CTF导航

相关文章

ItyFuzz：基于快照的智能合约模糊测试｜技术进展
admin
128
慢雾：警惕 Web3 钱包 WalletConnect 钓鱼风险
admin
332
智能合约-内联汇编操作码
admin
311
乱象重生中如何睡个好觉？
admin
422
DFX Finance遭重入攻击， 损失近400万美元
admin
411
迟到者的加密指南
admin
618

暂无评论

您必须登录才能参与评论！
立即登录
暂无评论...

相关文章

非法资金流动案例分析：$55M DAI 钓鱼事件
0
SDC2024 议题回顾 | 从硬件钱包到TrustZone：Web3密钥托管的安全挑战与解决方案
0
非法资金流动案例分析：Li.Fi Attack
0
零时科技 || Ramses 攻击事件分析
0
如何绕过数字钱包的安全支付机制 —— Usenix Security 24 论文导览
0
门罗币隐私保护之环签名
0
零时科技 || Radiant Capital 攻击事件分析
0
慢雾：Compound Finance V2 安全审计手册
0
新瓶装旧酒｜套利 MEV 机器人骗局
0
慢雾：貔貅盘防范指南
0